The Blocks Will Eventually Separate Again What Is the Final Velocity of the 55 Kg Block
Momentum and Collisions Review
Navigate to:
Office E: Problem-Solving
57. A 0.530-kg basketball game hits a wall head-on with a forwards speed of 18.0 m/s. It rebounds with a speed of thirteen.5 m/southward. The contact time is 0.100 seconds. (a) determine the impulse with the wall, (b) determine the forcefulness of the wall on the brawl.
Answer: Answer: (a) -xvi.7 N s; (b) -167 North
Given: thousand = 0.530 kg; vi = xviii.0 m/s; vf = 13.five m/s; t = 0.100 s
Notice: (a) Impulse, (b) Strength
(a) Impulse = Momentum Alter = 1000•Delta 5 = 1000•(vf - vi)= (0.530 kg)•( -13.5 1000/s - 18.0 thou/s)
Impulse = -sixteen.seven kg•k/due south = -16.7 N•s
where the "-" indicates that the impulse was reverse the original management of motion.
(Note that a kg•m/s is equivalent to a North•s)
(b) The impulse is the product of forcefulness and time. So if impulse is known and time is known, forcefulness can be easily determined.
Impulse = F•t
F = Impulse/t = (-16.vii N southward) / (0.100 s) = -167 N
where the "-" indicates that the impulse was opposite the original management of movement.
58. A 4.0-kg object has a frontwards momentum of 20. kg•m/southward. A 60. North•southward impulse acts upon information technology in the direction of motion for five.0 seconds. A resistive force of half dozen.0 North then impedes its motion for 8.0 seconds. Determine the final velocity of the object.
Answer: vf = 8.0 thou/south
This question is all-time thought near conceptually using the principle that an objects momentum is changed when it encounters an impulse and the amount of alter in momentum is equal to the impulse which it encounters.
Hither an object starts with 20 units (kg•m/s) of momentum. It then encounters an impulse of 60 units (Northward•due south) in the direction of motion. A threescore-unit impulse will change the momentum by threescore units, either increasing or decreasing it. If the impulse is in the direction of an object'south movement, then information technology volition increase the momentum. So now the object has 80 units (kg•m/s) of momentum. The object and then encounters a resistive force of vi.0 N for 8.0 s. This is equivalent to an impulse of 48 units (Due north•southward). Since this impulse is "resistive" in nature, it volition subtract the object's momentum by 48 units. The object now has 32 units of momentum. The question asks for the object's velocity after encountering these 2 impulses. Since momentum is the product of mass and velocity, the velocity can be easily determined.
vfinal = pfinal / thou = (32 kg m/due south) / (4.0 kg) = 8.0 m/s
59. A iii.0-kg object is moving frontwards with a speed of 6.0 g/s. The object then encounters a strength of 2.5 Due north for 8.0 seconds in the direction of its motion. The object then collides caput-on with a wall and heads in the opposite direction with a speed of five.0 m/s. Determine the impulse delivered by the wall to the object.
Answer: 53 N•south
Similar the previous trouble, this trouble is best solved by thinking through it conceptually using the impulse-momentum alter principle.
Here the object begins with a momentum of 18 units (kg•thousand/southward). The object encounters a force of 2.five Northward for 8.0 seconds. This is equivalent to an impulse of xx units (Northward•southward). Since this impulse acts in the direction of motion, it changes the object'southward momentum from 18 units to 38 units. A final impulse is encountered when colliding with a wall. Upon rebounding, the object has a momentum of -fifteen units (kg•m/southward). The -xv is the product of mass (iii kg) and velocity (-5 g/due south). The "-" sign is used since the object is at present moving in the contrary management as the original motion. The standoff with the wall inverse the object's momentum from +38 units to -15 units. Thus, the collision must have resulted in a 53-unit impulse since it altered the object's momentum by 53 units.
60. A 46-gram tennis ball is launched from a 1.35-kg bootleg cannon. If the cannon recoils with a speed of 2.1 m/due south, decide the cage speed of the lawn tennis brawl.
Answer: 62 m/s
Given: kball = 46 g = 0.046 kg; 1000cannon = 1.35 kg; vcannon = -2.1 grand/southward
Notice: vball = ???
The ball is in the cannon and both objects are initially at residuum. The total system momentum is initially 0. Subsequently the explosion, the total system momentum must as well be 0. Thus, the cannon'southward backward momentum must exist equal to the ball's forrard momentum.
(one.35 kg) • (-2.i m/due south) = (0.046 kg) • vball
vball = (1.35 kg) • (2.1 g/s) / (0.046 kg) = 61.63 grand/s = ~62 m/s
61. A two.0-kg box is attached past a cord to a 5.0-kg box. A compressed leap is placed betwixt them. The two boxes are initially at rest on a friction-free track. The string is cut and the jump applies an impulse to both boxes, setting them in motion. The ii.0-kg box is propelled backwards and moves 1.two meters to the cease of the rails in 0.fifty seconds. Determine the time it takes the five.0-kg box to move 0.90 meters to the opposite end of the runway.
Reply: 0.94 due south
For the sake of the discussion, the ii-kg box will exist referred to equally Box 1 and the 5-kg box will be referred to as box two.
Given: mbox 1 = ii.0 kg; mbox ii = 5.0 kg; dbox 1 = 1.2 m; tbox 1 = 0.50 s; dbox 2 = 0.90 one thousand
Find: tbox ii = ???
The two boxes are initially at rest. The total arrangement momentum is initially 0. Later the cutting of the string and the impulse of the spring, the total system momentum must too be 0. Thus, Box 1's astern momentum must be equal to the Box 2's forward momentum. The distance and time for Box ane must exist used to determine its velocity.
Now the principle of momentum conservation can be used to determine Box 2's velocity.
(2 kg) • (2.4 1000/s) = (5 kg) • vbox ii
vbox 2 = (ii kg) • (2.4 m/s) / (5 kg) = 0.96 m/s
The velocity of Box two can exist used to determine the time information technology takes it to move a distance of 0.ninety meters.
Time = dbox 2 / vbox two = (0.xc m) / (0.96 g/south) = 0.9375 s = ~0.94 s
62. Ii children are playing with a big snowball while on ice skates on a frozen pond. The 33-kg child tosses the five.0-kg snowball, imparting a horizontal speed of v.0 chiliad/s to information technology. The 33-kg child is four.0 meters from a 28-kg kid and 8.0 meters from the edge of the pond (located behind him). Assuming negligible friction, how much time elapses between when the 28-kg child gets hit by the snowball and when the 33-kg child reaches the edge of the pond?
Respond: 9.8 south
For the sake of the discussion, we will refer to the 33-kg child as the "thrower" and the 28-kg child equally the "catcher."
In this scenario, the thrower tosses a snowball forwards towards the catcher. This throwing action involves an impulse imparted to the snowball. And due to activeness-reaction, in that location is an identical impulse imparted to the thrower which causes the thrower to be set in motion in the contrary direction. The impulse is equal to the momentum modify. And since the mass and the velocity modify of the snowball are known, the momentum modify of the snowball can be determined.
thou • (Delta five)snowball = (5.0 kg) • (+ v.0 m/s - 0 m/s) = 25.0 kg•one thousand/southward
This 25-unit momentum modify of the snowball is equal to the thrower's momentum modify. Thus the thrower is moving backwards towards the edge of the pond with a momentum of -25.0 kg•one thousand/s. Since momentum is related to velocity, the mail service-impulse velocity tin can be determined.
5thrower = pthrower / mthrower
vthrower = (-25.0 kg•m/s) / (33 kg)
vthrower = -0.7576 one thousand/s
The thrower began 8.0 meters from the edge of the pond. In one case the ball has been thrown, the thrower is moving backwards towards the edge of the pond with a speed of 0.7576 k/s. Bold negligible friction on the icy pond, the speed tin can be used to make up one's mind the time that elapses between when the brawl is thrown and when the thrower reaches the pond's border.
t = d / five
tfor thrower to accomplish pond's border = (8.0 meters) / (0.7576 thousand/due south)
tfor thrower to attain pond'south edge = x.56 seconds
Once the brawl is thrown, the thrower starts moving backwards towards the swimming's edge. Meanwhile, the ball is moving forrad towards the catcher. The time for the brawl to movement from the thrower's original position to the catcher is dependent upon the ball's speed and the original distance betwixt the thrower and the catcher.
t = d / 5
tfor brawl to move from thrower to catcher = (iv.0 meters) / (five.0 m/s)
tfor brawl to move from thrower to catcher = 0.800 seconds
The instant the brawl is thrown, two motions occur - the brawl moves forrad towards the catcher and the thrower moves backwards towards the swimming's edge. The ball reaches the catcher in 0.800 seconds. And 9.76 seconds (~9.8 s) later (ten.56 s - 0.lxxx s), the thrower reaches the swimming's edge.
63. A 2.eight-kg physics cart is moving forrad with a speed of 45 cm/s. A 1.9-kg brick is dropped from rest and lands on the cart. The cart and brick motion together beyond the horizontal surface. Assume an isolated system.
a. Determine the post-collision speed of the cart and the brick.b. Make up one's mind the momentum change of the cart.
c. Determine the momentum alter of the brick.
d. Determine the internet impulse upon the cart.
due east. Determine the cyberspace impulse upon the system of cart and brick.
Answers: (a) 5 = 27 cm/s
(b) Delta pcart = -51 kg • cm/southward
(c) Delta pbrick = +51 kg • cm/south
(d) Impulse on cart = -51 kg • cm/south
(e) Impulse on brick = +51 kg • cm/s
Before the standoff, just the moving cart has momentum. The total momentum of the system is just the mass of the cart multiplied by the velocity of the cart.
ptotal-before = (2.eight kg) • (45 cm/southward)
ptotal-before = 126 kg • cm/south
The standoff is perfectly inelastic; the two objects stick together and movement as a single unit. Subsequently the collision, the total momentum of the organisation is the sum of the individual momentum values.
ptotal-subsequently = chiliadcart-subsequently • vcart-later + one thousandbrick • fivebrick-subsequently
pfull-later on = mcart-after • 5 + mbrick • v
ptotal-after = (2.8 kg) • 5 + (1.9 kg) • v
ptotal-afterwards = (4.vii kg) • v
Bold an isolated system, total system momentum is conserved. Thus, before- and after-collision momentum expressions can be set equal to each other, and the equation tin can be manipulated to solve for the postal service-standoff speed of the ii objects.
v = (126 kg • cm/s) / (4.7 kg)
v = 26.809 cm/s (~27 cm/s)
The momentum change of the cart (Delta pcart) is simply the difference between the initial and final momentum values.
Delta pcart = mcart-later on • vcart-after - grandcart • 5cart-before
Delta pcart = (2.eight kg) • (26.809 m/southward) - (2.viii kg) • (45 cm/s)
Delta pcart = -50.936 kg • cm/s (~51 kg•cm/southward)
During the standoff, the cart loses l.9 units of momentum. Since total system momentum is conserved, the brick must gain the same quantity of momentum.
The alter in momentum of the cart is due to the fact that an impulse acts upon the cart during the collision. The moment contact is made between the brick and the cart, the two objects are moving at different speeds relative to each other. Consequently, there will be a friction force acting between the two surfaces until the 2 objects maintain the same speed. That is, the brick will pull backward upon the moving cart in society to slow information technology down; and the moving cart will pull forward upon the stationary brick in order to speed it upward. These impulses are what cause the momentum changes. And these impulses are equal to the momentum changes. Thus,
Impulse on brick = Delta pbrick = +50.936 kg • cm/s (~51 kg•cm/s)
64. In a physics lab, a 0.500-kg cart moving at 36.iv cm/s collides inelastically with a second cart which is initially at residuum. The two carts move together with a speed of 21.8 cm/s after the collision. Make up one's mind the mass of the second cart.
Reply: ~ 0.335 kg
This problem involves a perfectly inelastic collision between two carts. Thus, the mail-standoff velocity of the two carts are identical. For advice sake, the carts will be referred to equally Cart A and Cart B. The given information is:
The unknown to be solved for in this problem is the mass of Cart B (kB).
The solution begins past setting the writing expressions for the total momentum of the system before and after the standoff.
Earlier Collision: ptotal-before = (0.500 kg)•(36.4 cm/southward) + (mB)•(0 cm/due south)After Standoff: ptotal-after = (0.500 kg)•(21.8 cm/s) + (gB)•(21.8 cm/s)
Assuming momentum conservation, these expressions are gear up equal to each other and and then algebraically manipulated to solve for the unknown (thousandB).
(0.500 kg)•(36.4 cm/south) = (0.500 kg)•(21.viii cm/s) + (mB)•(21.8 cm/s)
(0.500 kg)•(36.four cm/south) - (0.500 kg)•(21.8 cm/s) = (thouB)•(21.8 cm/southward)
(7.thirty kg•cm/due south) = (one thousandB)•(21.viii cm/s)
0.33486 kg = mB
mB = ~0.335 kg
65. A 9230-kg truck collides head on with a 1250-kg parked motorcar. The vehicles entangle together and slide a linear distance of 10.6 meters earlier coming to rest. Assuming a uniform coefficient of friction of 0.820 between the road surface and the vehicles, decide the pre-collision speed of the truck.
Answer: fourteen.viii m/s
Here is an case of a more difficult problem involving the combination of momentum principles with information learned in other units of the course. The trouble involves a perfectly inelastic collision between a truck and a car. Thus, the postal service-collision velocity of the truck and car are identical. The given standoff information is:
The unknown to be solved for in this problem is the velocity of the truck earlier the collision (vTruck-before).
In that location is some kinematic/dynamic information provided that volition help in determining the post-standoff velocity of the entangled truck and car.
The combination of car and truck will slide to a final resting position due to the action of friction. The coefficient of friction, a gratis-body diagram and a kinematic equation can be used to determine the velocity of the car and truck immediately following the collision.
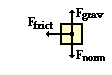The free-body diagram is shown at the correct. Note that the unbalanced force is friction. Its value is plant past multiplying the coefficient of friction past the combined weight of the car and truck (mu•One thousand•g where M = one thousandtruck + mmotorcar ). The force of friction is the cyberspace strength. Thus, the dispatch is the strength of friction divided by the combined mass of the automobile and the truck (M). Subsequently, the expression for the acceleration of the car and truck while sliding to a cease is simply mu•grand.
a = -8.036 m/s/due south
(The - sign indicates a deceleration or slowing down motion.)
At present a kinematic equation tin can be used to solve for the velocity of the motorcar and truck immediately after the standoff. This is shown below:
(0 chiliad/s)2 = fiveo 2 + 2•(-viii.036 thou/s/south)•(10.6 thou) = vo 2 - 170.36 thouii/southtwo
(0 m/s)2 = vo 2 - 170.36 one thousand2/s2
vo 2 = 170.36 m2/due south2
vo = SQRT(170.36 m2/s2)
vo = 13.052 m/s (= 5Truck-after = vCar-subsequently )
Now that the postal service-collision velocity of the automobile and truck are known, expressions for the total system momentum can be written for the before- and afterwards-collision situations.
Earlier Collision: ptotal-earlier = (9320 kg)•(vTruck-before) + (1250 kg)•(0 cm/s)After Collision: ptotal-afterwards = (9320 kg)•(13.052 m/south) + (1250 kg)•(13.052 yard/s)
Assuming momentum conservation, these expressions are fix equal to each other and then algebraically manipulated to solve for the unknown (kB).
(9320 kg)•(vTruck-before) = (9320 kg)•(13.052 one thousand/s) + (1250 kg)•(13.052 m/s)
(9320 kg)•(vTruck-before) = 137963 kg•m/s
(5Truck-before) = (137963 kg•m/south) / (9320 kg)
vTruck-before = ~xiv.8 m/s
66. A classic physics sit-in involves firing a bullet into a block of wood suspended by strings from the ceiling. The tiptop to which the woods rises below its lowest position is mathematically related to the pre-collision speed of the bullet. If a 9.7-gram bullet is fired into the center of a 1.1-kg block of wood and information technology rises upward a altitude of 33 cm, then what was the pre-standoff speed of the bullet?
Reply: ii.ix x ten2 m/s
Here is another instance in which momentum principles must be combined with content learned in other units in order to complete an assay of a physical situation. The standoff involves the inelastic collision between a block of woods and bullet. The bulled lodges into the wood and the two objects move with identical velocity after the collision. The kinetic energy of the woods and bullet is so converted to potential energy every bit the combination of two objects rises to a concluding resting position.
Energy conservation can exist used to determine the velocity of the wood-bullet combination immediately later the standoff. The kinetic free energy of the wood-bullet combination is set up equal to the terminal potential energy of the forest-bullet combination and the equation is manipulated to solve for the postal service-collision velocity of the forest-bullet combination. The work is shown here:
0.5 • vcombination-later two = (9.8 m/stwo) • (0.33 chiliad)
vcombination-afterward 2 = 2 •(9.viii thousand/s2) • (0.33 m)
vcombination-after 2 = 6.468 thoutwo/s2
vcombination-after = 2.5432 m/s
Now momentum conservation can be used to determine the pre-standoff velocity of the bullet (vbullet-before). The known information is:
Expressions for the total system momentum can be written for the before- and after-collision situations.
Before Collision: pfull-before = (i.1 kg)•(0 m/s) + (0.0097 kg)•(fivebullet-before)After Collision: ptotal-after = (i.1 kg)•(2.5432 m/s) + (0.0097 kg)•(2.5432 m/south)
Assuming momentum conservation, these expressions are set equal to each other and so algebraically manipulated to solve for the unknown (mB).
(0.0097 kg)•(fivebullet-before) = (1.1 kg)•(2.5432 m/s) + (0.0097 kg)•(2.5432 thou/s)
(0.0097 kg)•(fivebullet-before) = 2.8222 kg•m/s
vbullet-before = (2.8222 kg•k/southward) / (0.0097 kg)
5bullet-earlier = 290.95 thou/southward
5bullet-before = ~two.ix 10 x2 m/southward
67. At an amusement park, twin brothers Timmy (yard = fifty kg) and Jimmy (k = 62 kg) occupy divide 36-kg bumper cars. Timmy gets his car cruising at three.six m/southward and collides head-on with Jimmy who is moving the opposite direction at one.six m/south. After the collision, Timmy bounces backwards at 0.5 one thousand/southward. Assuming an isolated system, determine ...
a. ... Jimmy's post-collision speed.b. ... the percentage of original kinetic free energy which is lost as the result of the collision.
Answer: (a) v = ~2.0 m/s
(b) % KE Loss = ~lxx. %
(a) Expressions for the total momentum of the system before and later the collision can be written. For the earlier-collision expression, Timmy is assigned a positive velocity value and Jimmy is assigned a negative velocity value (since he is moving in the opposite direction). Furthermore, the mass of the bumper car must be figured into the total mass of the individually moving objects.
ptotal-earlier = gTimmy • vTimmy-before + mJimmy • vJimmy-earlier
ptotal-before = (86 kg) • (iii.6 k/south) + (98 kg) • (-1.6 m/s)
For the before-collision expression, Timmy is assigned a negative velocity value (since he has bounced backwards in the opposite direction of his original movement. Jimmy is assigned a velocity of v since his velocity is non known.
ptotal-after = mTimmy • fiveTimmy-after + mJimmy • fiveJimmy-after
ptotal-subsequently = (86 kg) • (-0.5 1000/south) + (98 kg) • (5Jimmy-after)
pfull-subsequently = (86 kg) • (-0.5 1000/south) + (98 kg) • v
Since the system is assumed to be isolated, the before-collision momentum expression can exist set equal to the after-collision momentum expression. The equation tin can then exist algebraically manipulated to solve for the post-collision velocity of Jimmy.
309.6 kg•1000/s - 156.8 kg•1000/s = (86 kg) • (-0.v m/s) + (98 kg) • v
152.8 kg•1000/s = - 43 kg•k/s + (98 kg) • v
152.8 kg•m/s + 43 kg•thousand/s = (98 kg) • v
195.8 kg•1000/s = (98 kg) • v
v = (195.viii kg•m/s) / (98 kg)
5 = ane.998 m/s = ~2.0 one thousand/southward
(b) This collision is neither perfectly rubberband (since the collision forcefulness is a contact force) nor perfectly inelastic (since the objects practise non stick together). Information technology is a partially elastic/inelastic collision. Since the collision is not perfectly elastic, in that location is a loss of total system kinetic free energy during the standoff. The earlier-collision and after-collision kinetic energy values tin can exist calculated and the per centum of full KE lost tin be adamant.
The before-standoff KE is based on earlier-standoff speeds:
KEsystem-before = 0.5 • yardTimmy • vTimmy -before 2 + 0.5 • mJimmy • 5Jimmy-before 2
KEorganization-earlier = 0.five • (86 kg) • (3.6 thou/s)2 + 0.five • (98 kg) • (1.6 grand/south)2
KEsystem-before = 557.28 J + 125.44 J
KEorganization-earlier = 682.72 J
The later on-collision KE is based on after -standoff speeds:
KEorganisation-later on = 0.5 • mTimmy • vTimmy-afterward + 0.5 • kJimmy • vJimmy-after
KEsystem-after = 0.v • (86 kg) • (0.5 m/s)2 + 0.5 • (98 kg) • (1.998 k/s)two
KEorganisation-after = 10.75 J + 195.61 J
KEsystem-afterward = 206.36 J
The organisation kinetic energy is changed from 682.72 J to 206.36 J during the collision. The total KE lost is 476.36 J. This value can be used to determine the percent of the original KE which is lost in the collision.
% KE Loss = 69.77% = ~70%
68. 2 billiard balls, assumed to have identical mass, collide in a perfectly rubberband collision. Ball A is heading Eastward at 12 grand/s. Ball B is moving West at 8.0 1000/s. Determine the post-collision velocities of Brawl A and Ball B.
Answer: fiveA-after = -8.0 cm/s; vB-after = 12 cm/s (The - indicates West and the + indicates East)
This standoff is said to be perfectly elastic. Thus, both the total system momentum and the total system kinetic energy of the two objects is conserved. The momentum conservation equation can be written every bit
Since the balls are identical, their masses are the same. That is, mA = mB = thousand. The equation can be rewritten as:
Since each term of the equation contains the variable 1000, we tin divide through by m and cancel m's from the equation. The equation tin can be rewritten equally:
vA-earlier + vB-earlier = fiveA-after + 5B-after For elastic collisions, total system kinetic energy is conserved. The kinetic energy conservation equation is written as
As shown in the book, this equation can be simplified to the grade of
vA-before + vA-after = vB-before + fiveB-later on The problem states the before-collision velocities of the ii assurance.
5B-earlier = - 8 cm/s (the - indicates west)
These two values can be substituted into equations one and 2 in a higher place.
12 cm/s - 8 cm/southward = fiveA-after + vB-after 
12 cm/s + fiveA-after = - 8 cm/south + 5B-afterward
Now the problem has been reduced to two equations and ii unknowns. Such a problem can be solved in numerous ways. One method involved using Equation 3 to develop an expression for vA-later on in terms of vB-after. This expression for vA-after can then exist substituted into Equation 4. The value of vB-after tin then be determined. This is shown below.
From Equation 3:
fiveA-afterwards = 4 cm/due south - vB-afterward
This expression for fiveA-after in terms of vB-later can now exist substituted into equation 4. This is shown below. The subsequent algebraic manipulation is shown too.
12 cm/south + 4 cm/s + viii cm/southward - 5B-after = + vB-after
24 cm/s = + fiveB-after + fiveB-afterward
24 cm/due south = 2 fiveB-afterward
vB-after = +12 cm/s
Now that the value of vB-after has been determined, it tin can be substituted into the original expression for fiveA-subsequently (Equation 5) in order to determine the numerical value of fiveA-afterward. This is shown below.
5A-after = 4 cm/due south - 12 cm/due south
vA-after = -eight.0 cm/s
69. A 1.72-kg block of soft wood is suspended by two strings from the ceiling. The wood is free to rotate in pendulum-similar fashion when a force is exerted upon it. A 8.l-k bullet is fired into the wood. The bullet enters the forest at 431 thousand/s and exits the opposite side shortly thereafter. If the woods rises to a top of 13.eight cm, then what is the exit speed of the bullet?
Answer: vbullet-after = 98.ii thousand/s
The difficulty of this problem lies in the fact that data from other units (work and energy) must exist combined with the momentum information from this unit of measurement to go far at a solution to the problem. In this scenario there is a collision between a stationary block of wood and a moving bullet. The impulse causes the block of wood to exist set up into move and the bullet to dull down. Momentum can be assumed to exist conserved. Once prepare into motion, the block of wood rises in pendulum-similar fashion to a given height. Its energy of motion (kinetic energy) is transformed into energy of vertical position (potential free energy). The mail service-standoff speed of the wood tin be determined using energy conservation equations.
To begin the solution, the concluding acme of the wood is used to determine the post-collision speed of the forest.
0.v • mwood •vwood 2 = mforest • one thousand • hforest
vwood 2 = 2 • g • hwood
vwoods = SQRT(2 • one thousand • hwood)
5woods = SQRT[two • (9.8 chiliad/s2) • (0.138 thou)]
5wood = SQRT[2.7048 m2/sii]
vwood = 1.6446 m/s
Immediately following the emergence of the bullet from the wood, the wood cake is moving with a speed of 1.6446 grand/s. Knowing this, momentum conservation can exist applied to determine the post-collision speed of the bullet.
where vwood-earlier = 0 m/s; vbullet-before = 431 m/s; vwood-after = ane.6446 m/due south; vbullet-afterwards = ???
(1.72 kg) • (0 grand/due south) + (0.00850 kg) • (431 1000/s) = (1.72 kg) • (i.6446 m/due south) + (0.00850 kg) • vbullet-afterward
(To simplify the work, the units will be dropped from the solution in the next several steps. Once a fivebullet-later on value is found, its units volition be in one thousand/due south, consistent with the units stated in the higher up line.)
0 + 3.6635 = 2.8288 + 0.00850 • vbullet-afterward
0.8347 = 0.00850 • fivebullet-after
(0.8347) / (0.00850) = vbullet-later on
vbullet-after = 98.205 m/s = ~98.2 yard/s
70. In a physics lab, the pitching speed of a student is adamant by throwing a baseball into a box and observing the box'southward motion after the grab. A measurement of the the distance the box slides across a crude surface of known coefficient of friction will allow 1 to make up one's mind the pre-impact speed of the pitched ball. If a 0.256-kg brawl hits a 3.46-kg box and the ball and box slide a distance of ii.89 meters beyond a surface with a coefficient of friction of 0.419, then what is the pre-impact speed of the pitched brawl?
Answer: seventy.7 1000/s
This is some other example of a problem in which information from other units (piece of work and free energy or Newton'due south laws and kinematics) must exist combined with the momentum information from this unit of measurement to arrive at a solution to the trouble. At that place is a collision between a stationary box and a moving baseball game that causes the baseball to tedious down and the box to speed up. It is a perfectly inelastic standoff with the baseball remaining lodged in the box and the two objects moving together with the same post-collision speed. Later the standoff occurs, the baseball game and box slide a given distance across a crude surface to a concluding resting position. The coefficient of friction between the box and the surface is given. This latter data (sliding altitude and mu value) can exist used to determine the mail-collision speed of the box and baseball. In one case found, momentum conservation can be practical to the collision to determine the pre-standoff speed of the baseball.
Piece of work and energy principles will be used to analyze the motion of the box/baseball system sliding to a stop. (Newton's laws and kinematics could merely every bit easily been used). Immediately following the standoff, the box/baseball system has kinetic energy. Friction does piece of work upon the box/baseball system to bring to a concluding resting position, characterized by zilch kinetic energy. The motion occurs across a level surface, and so at that place is no potential free energy change of the box. The work done by friction is equal to the kinetic free energy change of the box/baseball system.
Ffrict • d • cos(Theta) = KEterminal - KEinitial
(mu •Fnorm) • d • cos(180) = 0.five • m •fivefinal ii - 0.v • m •5initial 2
- (mu • m • chiliad) • d = 0 - 0.v • thousand • vinitial ii
mu • one thousand • d = 0.five • 5initial two
ii •mu • chiliad • d = vinitial 2
SQRT(2 • mu • k • d) = vinitial
where mu = 0.419; d = two.89 m; and g = nine.8 m/sii
vinitial = SQRT[2 • (0.419) • (9.8 1000/s2 ) • (2.89 yard)]
vinitial = SQRT[23.734 m2/s2]
5initial = iv.8717 m/southward
Immediately following the standoff, the box/baseball system begins moving with a speed of 4.8717 m/south. Now momentum conservation can exist practical to determine the pre-collision speed of the baseball.
(0.256 kg) • vbaseball game-before + (three.46 kg) • (0 g/s) = (0.256 kg) • (4.8717 m/s) + (iii.46 kg) • (4.8717 k/s)
(To simplify the solution, the units volition be dropped from the solution in the side by side several steps. Once a vbaseball-earlier value is found, its units volition exist in m/due south, consistent with the units stated in the higher up line.)
0.256 • vbaseball-before = 1.2472 + xvi.8562
0.256 • vbaseball-before = 18.1033
fivebaseball-before = (xviii.1033) / (0.256)
5baseball game-before = lxx.7 m/due south
71. Two ice skaters collide on the ice. A 39.vi-kg skater moving S at 6.21 m/s collides with a 52.i-kg skater moving East at 4.33 1000/southward. The two skaters entangle and move together across the ice. Determine the magnitude and direction of their post-collision velocity.
Reply: three.64 m/due south at 42.v degrees e of s (312.v degrees)
The difficulty of this problem lies in the fact that the standoff occurs between two objects moving at right angles to each other. Thus, vector principles volition take to be combined with momentum principles to arrive at a solution to the problem. The aforementioned conservation of momentum principle volition be used; merely when summing the before momentum values of the two objects, the fact that they are at right angles to each means that they volition have to exist added using the Pythagorean theorem. The standoff is perfectly inelastic with the two skaters moving at the same speed after the collision. For communication sake, the 39.6-kg skater will be referred to as skater A and the 52.1-kg skater will exist referred to as skater B. A vector diagram will likely help in the solution of the trouble.
The private momentum of the two skaters is get-go determined.
pB = mB • B = (52.1 kg) • (4.33 m/south, East ) = 225.593 kg • m/due south, Due east
At present the Pythagorean theorem can exist used to add these two vectors and thus determine the pre-collision organization momentum. The diagram at the right shows the vectors existence added in head-to-tail fashion. The resultant is drawn from the tail of the start vector to the head of the last vector. The resultant is the hypotenuse of a right triangle whose sides are the pA and pB vectors.
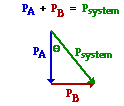psystem = pA + pB (where pA and pB are right bending vectors) psystem = SQRT(pA ii+ pB 2)
psystem = SQRT[(245.916 kg • one thousand/due south)2+ (225.593 kg • m/s)2]
parrangement = 333.717 kg • m/s
The management of the this full organization momentum vector can be adamant past using a trigonometric office. As shown in the diagram above, the angle theta is the angle between the system momentum vector and the vertical. This angle can be determined using either the tangent, cosine or sine function. The tangent function is used below.
tangent(Theta) = pB / pA
tangent(Theta) = (225.593 kg • m/s) / (245.916 kg • yard/s)
tangent(Theta) = 0.91735
Theta = tan-i (0.91735)
Theta = 42.532 degrees
Earlier the collision, the total organization momentum is 333.717 kg • yard/south in a direction of 42.532 degrees eastward of due south. Since total system momentum is conserved, the after-collision momentum of the system is also 333.717 kg • chiliad/s in a direction of 42.532 degrees east of southward. After the collision, the ii objects move together as a single unit of measurement with the same velocity. The velocity of each object can be found by dividing the full momentum by the full mass.
vorganization = ( psystem ) / (chiliadsystem )
vsystem = (333.717 kg • m/s) / (91.7 kg)
vsystem = three.64 m/s at 42.five degrees east of southward
72. In a physics lab, two carts collide elastically on a level, low-friction track. Cart A has a mass of 1.500 kg and is moving due east at 36.five cm/due south. Cart B has a mass of 0.500 kg and is moving Westward at 42.viii cm/s. Determine the mail service-collision velocities of the two carts.
Respond: fiveA-after = -three.fifteen cm/s; fiveB-afterwards = 76.15 cm/s
This is a perfectly elastic standoff in which both momentum and kinetic free energy are conserved. The method for solving this problem will exist very similar to that used in Trouble #68 in a higher place. Two equations will be developed using the momentum conservation and kinetic energy conservation principles. One equation volition exist used to develop an expression for 5A in terms of vB. This expression will then be substituted into the 2d equation in order to solve for vB. The original vA expression tin and then exist used to determine the vA value. The solution is shown beneath.
The momentum conservation equation can exist written every bit
(i.500 kg) • (+36.5 cm/s) + (0.500 kg) • (-42.8 cm/s) = (1.500 kg) • fiveA-later on + (0.500 kg) • fiveB-after
33.35 kg • cm/s = (i.500 kg) • 5A-after + (0.500 kg) • fiveB-subsequently
For elastic collisions, total system kinetic free energy is conserved. The kinetic energy conservation equation is written as
As shown in the book, this equation tin exist simplified to the form of
36.v cm/south + vA-after = -42.8 cm/southward + vB-after
fiveA-later = vB-after - 79.3 cm/s
Now the problem has been reduced to two equations and two unknowns. Such a problem can be solved in numerous ways. Note that equation 2 represents an expression for fiveA-after in terms of fiveB-after. This expression for vA-after tin can then be substituted into Equation 1. The value of fiveB-after can so be determined. This work is shown below. (To simplify the mathematics, the units will be dropped from the numerical values stated in the solution. When fiveB-afterward is solved for, its units will be in cm/s - the same units used for velocity in the above portion of the solution.)
33.35 = i.500 • fiveB-after - 118.95 + 0.500 • vB-after
152.xxx = two.00 • vB-after
vB-later = 76.fifteen cm/s
Now that the value of 5B-subsequently has been determined, it tin be substituted into the original expression for vA-later (Equation 2) in order to make up one's mind the numerical value of vA-after. This is shown below.
vA-after = 76.15 cm/s - 79.3 cm/s
vA-after = -iii.15 cm/s
[ #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 | #67 | #68 | #69 | #70 | #71 | #72 ]
Navigate to:
You Might Also Like ...
Users of The Review Session are often looking for learning resource that provide them with exercise and review opportunities that include built-in feedback and didactics. If that is what you're looking for, then y'all might also like the following:
- The Calculator Pad
The Computer Pad includes physics word problems organized by topic. Each problem is accompanied by a popular-up respond and an sound file that explains the details of how to approach and solve the trouble. It'due south a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Estimator Pad Home | Calculator Pad - Momentum and Collisions
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further cleaved downwardly into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-similar surround. It is available for phones, tablets, Chromebooks, and Macintosh computers. It'due south a perfect resource for those wishing to refine their conceptual reasoning abilities. Part three of the series includes topics in Momentum and Collisions.
Visit: MOP the App Home || MOP the App - Office iii
Source: https://www.physicsclassroom.com/reviews/momentum/momans4.cfm
0 Response to "The Blocks Will Eventually Separate Again What Is the Final Velocity of the 55 Kg Block"
Post a Comment